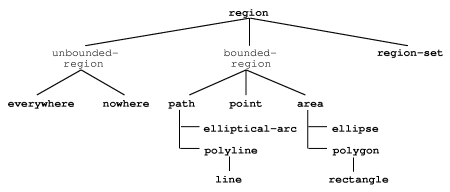
3.2 Other Region Types
The other types of regions are points, polylines, polygons, elliptical arcs, and ellipses. All of these region types are closed under affine transformations. [annotate]
Major issue: There is a proposal to remove the polygon, polyline, line, ellipse, and elliptical-arc classes, since they are only of limited utility, and CLIM itself doesn't use the classes at all. The advantage of removing these classes is that both the spec and CLIM itself become a little simpler, and there are fewer cases of the region protocol to implement. However, removing these classes results in a geometric model that is no longer closed (in the mathematical sense). This lack of closure makes it difficult to specify the design-based drawing model. Furthermore, these are intuitive objects that are used by a small, but important, class of applications, and some people feel that CLIM should relieve programmers from having to implement these classes for himself or herself. [annotate]
The advocates of of removing these classes also propose removing the design-based drawing model. In this case, a more consistent proposal is to remove all of the geometric classes, including point and rectangle. [annotate]
Again, the opposing point of view believes that the power and flexibility of the design-based drawing model does not justify the removal of any of these classes. One counter-proposal is to require CLIM not to use any of the extended region classes internally, and to move the implementation of the extended region classes to a separately loadable module (via provide and require). --- SWM, York [annotate]
3.2.1 Points
A point is a mathematical point in the plane, designated by its coordinates, which are a pair of real numbers (where a real number is defined as either an integer, a ratio, or a floating point number). Points have neither area nor length (that is, they have dimensionality 0). [annotate]
[point, Concept← A Glossary]
[point, Concept← 12.5.2 Compound Drawing Functions, draw-arrow]
[point, Concept← 12.5.1 Basic Drawing Functions, draw-text]
[point, Concept← 12.5.1 Basic Drawing Functions, draw-ellipse]
[point, Concept← 12.5.1 Basic Drawing Functions, draw-line]
[point, Concept← 12.5.1 Basic Drawing Functions, draw-point]
[point, Concept← 3.2.5 Ellipses and Elliptical Arcs, make-elliptical-arc]
[point, Concept← 3.2.5 Ellipses and Elliptical Arcs, make-ellipse]
[point, Concept← 3.2.4 Rectangles, make-rectangle]
[point, Concept← 3.2.4 Rectangles, make-rectangle]
[point, Concept← 3.2.1.1 The Point Protocol, point-x]
[point, Concept← 3.2.1 Points, pointp]
Note well that a point is not a pixel; CLIM models a drawing plane with continuous coordinates. This is discussed in more detail in Chapter 12. [annotate]
The protocol class that corresponds to a mathematical point. This is a subclass of region and bounding-rectangle. If you want to create a new class that behaves like a point, it should be a subclass of point. All instantiable subclasses of point must obey the point protocol. [annotate] |
Returns true if object is a point, otherwise returns false. [annotate] |
An instantiable class that implements a point. This is a subclass of point. This is the class that make-point instantiates. Members of this class are immutable. [annotate] |
Returns an object of class standard-point whose coordinates are x and y. x and y must be real numbers. [annotate] |
3.2.1.1 The Point Protocol
The following generic functions comprise the point API. Only point-position is in the point protocol, that is, all classes that are subclasses of point must implement methods for point-position, but need not implement methods for point-x and point-y. [annotate]
Returns both the x and y coordinates of the point point as two values. [annotate] |
Returns the x or y coordinate of the point point, respectively. CLIM will supply default methods for point-x and point-y on the protocol class point that are implemented by calling point-position. [annotate] |
3.2.2 Polygons and Polylines
A polyline is a path that consists of one or more line segments joined consecutively at their end-points. [annotate]
[polyline, Concept← 3.2.2.1 The Polygon and Polyline Protocol]
[polyline, Concept← 3.2.2 Polygons and Polylines, polylinep]
Polylines that have the end-point of their last line segment coincident with the start-point of their first line segment are called closed; this use of the term "closed" should not be confused with closed sets of points. [annotate]
A polygon is an area bounded by a closed polyline. [annotate]
[polygon, Concept← 3.2.2.1 The Polygon and Polyline Protocol]
[polygon, Concept← 3.2.2 Polygons and Polylines, polygonp]
If the boundary of a polygon intersects itself, the odd-even winding-rule defines the polygon: a point is inside the polygon if a ray from the point to infinity crosses the boundary an odd number of times. [annotate]
The protocol class that corresponds to a polyline. This is a subclass of path. If you want to create a new class that behaves like a polyline, it should be a subclass of polyline. All instantiable subclasses of polyline must obey the polyline protocol. [annotate] |
Returns true if object is a polyline, otherwise returns false. [annotate] |
An instantiable class that implements a polyline. This is a subclass of polyline. This is the class that make-polyline and make-polyline* instantiate. Members of this class are immutable. [annotate] |
Returns an object of class standard-polyline consisting of the segments connecting each of the points in point-seq (or the points represented by the coordinate pairs in coord-seq). point-seq is a sequence of points; coord-seq is a sequence of coordinate pairs, which are real numbers. It is an error if coord-seq does not contain an even number of elements. [annotate] If closed is true, then the segment connecting the first point and the last point is included in the polyline. The default for closed is false. [annotate] This function is permitted to capture its mutable inputs; the consequences of modifying those objects are unspecified. [annotate] |
The protocol class that corresponds to a mathematical polygon. This is a subclass of area. If you want to create a new class that behaves like a polygon, it should be a subclass of polygon. All instantiable subclasses of polygon must obey the polygon protocol. [annotate] |
Returns true if object is a polygon, otherwise returns false. [annotate] |
An instantiable class that implements a polygon. This is a subclass of polygon. This is the class that make-polygon and make-polygon* instantiate. Members of this class are immutable. [annotate] |
Returns an object of class standard-polygon consisting of the area contained in the boundary that is specified by the segments connecting each of the points in point-seq (or the points represented by the coordinate pairs in coord-seq). point-seq is a sequence of points; coord-seq is a sequence of coordinate pairs, which are real numbers. It is an error if coord-seq does not contain an even number of elements. [annotate] This function is permitted to capture its mutable inputs; the consequences of modifying those objects are unspecified. [annotate] |
3.2.2.1 The Polygon and Polyline Protocol
The following generic functions comprise the polygon and polyline protocol. All classes that are subclasses of either polygon or polyline must implement methods for these generic functions. Some of the functions below take an argument named polygon-or-polyline; this argument may be either a polygon or a polyline. [annotate]
Returns a sequence of points that specify the segments in polygon-or-polyline. This function returns objects that reveal CLIM's internal state; do not modify those objects. [annotate] |
Applies function to all of the coordinates of the vertices of polygon-or-polyline. function is a function of two arguments, the x and y coordinates of the vertex; it has dynamic extent. [annotate] |
Applies function to the segments that compose polygon-or-polyline. function is a function of four arguments, the x and y coordinates of the start of the segment, and the x and y coordinates of the end of the segment; it has dynamic extent. When map-over-polygon-segments is called on a closed polyline, it will call function on the segment that connects the last point back to the first point. [annotate] |
Returns true if the polyline polyline is closed, otherwise returns false. This function need be implemented only for polylines, not for polygons. [annotate] |
3.2.3 Lines
A line is a polyline consisting of a single segment. [annotate]
The protocol class that corresponds to a mathematical line segment, that is, a polyline with only a single segment. This is a subclass of polyline. If you want to create a new class that behaves like a line, it should be a subclass of line. All instantiable subclasses of line must obey the line protocol. [annotate] |
Returns true if object is a line, otherwise returns false. [annotate] |
An instantiable class that implements a line segment. This is a subclass of line. This is the class that make-line and make-line* instantiate. Members of this class are immutable. [annotate] |
Returns an object of class standard-line that connects the two points start-point and end-point (or the positions (start-x,start-y) and (end-x,end-y)). [annotate] This function is permitted to capture its mutable inputs; the consequences of modifying those objects are unspecified. [annotate] |
3.2.3.1 The Line Protocol
The following generic functions comprise the line API. Only line-start-point* and line-end-point* are in the line protocol, that is, all classes that are subclasses of line must implement methods for line-start-point* and line-end-point*, but need not implement methods for line-start-point and line-end-point. [annotate]
Returns the starting or ending point, respectively, of the line line as two real numbers representing the coordinates of the point. [annotate] |
Returns the starting or ending point of the line line, respectively. [annotate] CLIM will supply default methods for line-start-point and line-end-point on the protocol class line that are implemented by calling line-start-point* and line-end-point*. [annotate] |
3.2.4 Rectangles
Rectangles whose edges are parallel to the coordinate axes are a special case of polygon that can be specified completely by four real numbers (x1,y1,x2,y2). They are not closed under general affine transformations (although they are closed under rectilinear transformations). [annotate]
The protocol class that corresponds to a mathematical rectangle, that is, rectangular polygons whose sides are parallel to the coordinate axes. This is a subclass of polygon. If you want to create a new class that behaves like a rectangle, it should be a subclass of rectangle. All instantiable subclasses of rectangle must obey the rectangle protocol. [annotate] [← 4.1.1 The Bounding Rectangle Protocol, bounding-rectangle] [← 4.1 Bounding Rectangles, standard-bounding-rectangle] [← 4.1 Bounding Rectangles, bounding-rectangle] [← 3.2.4.1 The Rectangle Protocol, rectangle-width] [← 3.2.4.1 The Rectangle Protocol, rectangle-min-x] [← 3.2.4.1 The Rectangle Protocol, rectangle-min-point] [← 3.2.4.1 The Rectangle Protocol] [← 3.2.4 Rectangles, standard-rectangle] [← 3.2 Other Region Types] |
Returns true if object is a rectangle, otherwise returns false. [annotate] |
An instantiable class that implements an axis-aligned rectangle. This is a subclass of rectangle. This is the class that make-rectangle and make-rectangle* instantiate. Members of this class are immutable. [annotate] |
Returns an object of class standard-rectangle whose edges are parallel to the coordinate axes. One corner is at the point point1 (or the position (x1,y1)) and the opposite corner is at the point point2 (or the position (x2,y2)). There are no ordering constraints among point1 and point2 (or x1 and x2, and y1 and y2). [annotate] Most CLIM implementations will choose to represent rectangles in the most efficient way, such as by storing the coordinates of two opposing corners of the rectangle. Because this representation is not sufficient to represent the result of arbitrary transformations of arbitrary rectangles, CLIM is allowed to return a polygon as the result of such a transformation. (The most general class of transformations that is guaranteed to always turn a rectangle into another rectangle is the class of transformations that satisfy rectilinear-transformation-p.) [annotate] This function is permitted to capture its mutable inputs; the consequences of modifying those objects are unspecified. [annotate] |
3.2.4.1 The Rectangle Protocol
The following generic functions comprise the rectangle API. Only rectangle-edges* is in the rectangle protocol, that is, all classes that are subclasses of rectangle must implement methods for rectangle-edges*, but need not implement methods for the remaining functions. [annotate]
Returns the coordinates of the minimum x and y and maximum x and y of the rectangle rectangle as four values, min-x, min-y, max-x, and max-y. [annotate] |
Returns the min point and max point of the rectangle rectangle, respectively. The position of a rectangle is specified by its min point. [annotate] CLIM will supply default methods for rectangle-min-point and rectangle-max-point on the protocol class rectangle that are implemented by calling rectangle-edges*. [annotate] |
| rectangle-min-x | rectangle | [Generic Function] |
| rectangle-min-y | rectangle | [Generic Function] |
| rectangle-max-x | rectangle | [Generic Function] |
| rectangle-max-y | rectangle | [Generic Function] |
Returns (respectively) the minimum x and y coordinate and maximum x and y coordinate of the rectangle rectangle. [annotate] CLIM will supply default methods for these four generic functions on the protocol class rectangle that are implemented by calling rectangle-edges*. [annotate] |
| rectangle-width | rectangle | [Generic Function] |
| rectangle-height | rectangle | [Generic Function] |
| rectangle-size | rectangle | [Generic Function] |
rectangle-width returns the width of the rectangle rectangle, which is the difference between the maximum x and its minimum x. rectangle-height returns the height, which is the difference between the maximum y and its minimum y. rectangle-size returns two values, the width and the height. [annotate] CLIM will supply default methods for these four generic functions on the protocol class rectangle that are implemented by calling rectangle-edges*. [annotate] |
3.2.5 Ellipses and Elliptical Arcs
An ellipse is an area that is the outline and interior of an ellipse. Circles are special cases of ellipses. [annotate]
[ellipse, Concept← 3.2.5.1 The Ellipse and Elliptical Arc Protocol]
[ellipse, Concept← 3.2.5 Ellipses and Elliptical Arcs, ellipsep]
An elliptical arc is a path consisting of all or a portion of the outline of an ellipse. Circular arcs are special cases of elliptical arcs. [annotate]
[elliptical arc, Concept← 3.2.5.1 The Ellipse and Elliptical Arc Protocol]
[elliptical arc, Concept← 3.2.5 Ellipses and Elliptical Arcs, elliptical-arc-p]
An ellipse is specified in a manner that is easy to transform, and treats all ellipses on an equal basis. An ellipse is specified by its center point and two vectors that describe a bounding parallelogram of the ellipse. The bounding parallelogram is made by adding and subtracting the vectors from the the center point in the following manner: [annotate]
| x coordinate | y coordinate | |
| Center of Ellipse | xc | yc |
| Vectors | dx1 | dy1 |
| dx2 | dy2 | |
| Corners of Parallelogram | xc + dx1 + dx2 | yc + dy1 + dy2 |
| xc + dx1 - dx2 | yc + dy1 - dy2 | |
| xc - dx1 - dx2 | yc - dy1 - dy2 | |
| xc - dx1 + dx2 | yc - dy1 + dy2 |
Note that several different parallelograms specify the same ellipse. One parallelogram is bound to be a rectangle---the vectors will be perpendicular and correspond to the semi-axes of the ellipse. [annotate]
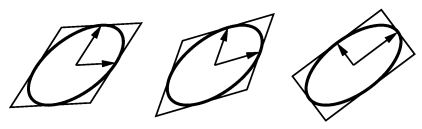
The special case of an ellipse with its axes aligned with the coordinate axes can be obtained by setting dx2 = dy1 = 0 or dx1 = dy2 = 0. [annotate]
The protocol class that corresponds to a mathematical ellipse. This is a subclass of area. If you want to create a new class that behaves like an ellipse, it should be a subclass of ellipse. All instantiable subclasses of ellipse must obey the ellipse protocol. [annotate] |
Returns true if object is an ellipse, otherwise returns false. [annotate] |
An instantiable class that implements an ellipse. This is a subclass of ellipse. This is the class that make-ellipse and make-ellipse* instantiate. Members of this class are immutable. [annotate] |
| make-ellipse | center-point radius-1-dx radius-1-dy radius-2-dx radius-2-dy &key start-angle end-angle | [Function] |
| make-ellipse* | center-x center-y radius-1-dx radius-1-dy radius-2-dx radius-2-dy &key start-angle end-angle | [Function] |
Returns an object of class standard-ellipse. The center of the ellipse is at the point center-point (or the position (center-x,center-y)). [annotate] Two vectors, (radius-1-dx,radius-1-dy) and (radius-2-dx,radius-2-dy) specify the bounding parallelogram of the ellipse as explained above. All of the radii are real numbers. If the two vectors are collinear, the ellipse is not well-defined and the ellipse-not-well-defined error will be signalled. The special case of an ellipse with its axes aligned with the coordinate axes can be obtained by setting both radius-1-dy and radius-2-dx to 0. [annotate] If start-angle or end-angle are supplied, the ellipse is the "pie slice" area swept out by a line from the center of the ellipse to a point on the boundary as the boundary point moves from the angle start-angle to end-angle. Angles are measured counter-clockwise with respect to the positive x axis. If end-angle is supplied, the default for start-angle is 0; if start-angle is supplied, the default for end-angle is 2π; if neither is supplied then the region is a full ellipse and the angles are meaningless. [annotate] This function is permitted to capture its mutable inputs; the consequences of modifying those objects are unspecified. [annotate] |
The protocol class that corresponds to a mathematical elliptical arc. This is a subclass of path. If you want to create a new class that behaves like an elliptical arc, it should be a subclass of elliptical-arc. All instantiable subclasses of elliptical-arc must obey the elliptical arc protocol. [annotate] |
Returns true if object is an elliptical arc, otherwise returns false. [annotate] |
An instantiable class that implements an elliptical arc. This is a subclass of elliptical-arc. This is the class that make-elliptical-arc and make-elliptical-arc* instantiate. Members of this class are immutable. [annotate] |
| make-elliptical-arc | center-point radius-1-dx radius-1-dy radius-2-dx radius-2-dy &key start-angle end-angle | [Function] |
| make-elliptical-arc* | center-x center-y radius-1-dx radius-1-dy radius-2-dx radius-2-dy &key start-angle end-angle | [Function] |
Returns an object of class standard-elliptical-arc. The center of the ellipse is at the point center-point (or the position (center-x,center-y)). [annotate] Two vectors, (radius-1-dx,radius-1-dy) and (radius-2-dx,radius-2-dy), specify the bounding parallelogram of the ellipse as explained above. All of the radii are real numbers. If the two vectors are collinear, the ellipse is not well-defined and the ellipse-not-well-defined error will be signalled. The special case of an elliptical arc with its axes aligned with the coordinate axes can be obtained by setting both radius-1-dy and radius-2-dx to 0. [annotate] If start-angle and start-angle are supplied, the arc is swept from start-angle to end-angle. Angles are measured counter-clockwise with respect to the positive x axis. If end-angle is supplied, the default for start-angle is 0; if start-angle is supplied, the default for end-angle is 2π; if neither is supplied then the region is a closed elliptical path and the angles are meaningless. [annotate] This function is permitted to capture its mutable inputs; the consequences of modifying those objects are unspecified. [annotate] |
3.2.5.1 The Ellipse and Elliptical Arc Protocol
The following functions apply to both ellipses and elliptical arcs. In all cases, the name elliptical-object means that the argument may be an ellipse or an elliptical arc. These generic functions comprise the ellipse protocol. All classes that are subclasses of either ellipse or elliptical-arc must implement methods for these functions. [annotate]
Returns the center point of elliptical-object as two values representing the coordinate pair. [annotate] |
Returns the center point of elliptical-object. [annotate] ellipse-center-point is part of the ellipse API, but not part of the ellipse protocol. CLIM will supply default methods for ellipse-center-point on the protocol classes ellipse and elliptical-arc that are implemented by calling ellipse-center-point*. [annotate] |
Returns four values corresponding to the two radius vectors of elliptical-arc. These values may be canonicalized in some way, and so may not be the same as the values passed to the constructor function. [annotate] |
Returns the start angle of elliptical-object. If elliptical-object is a full ellipse or closed path then ellipse-start-angle will return nil; otherwise the value will be a number greater than or equal to zero, and less than 2π. [annotate] |
Returns the end angle of elliptical-object. If elliptical-object is a full ellipse or closed path then ellipse-end-angle will return nil; otherwise the value will be a number greater than zero, and less than or equal to 2π. [annotate] |